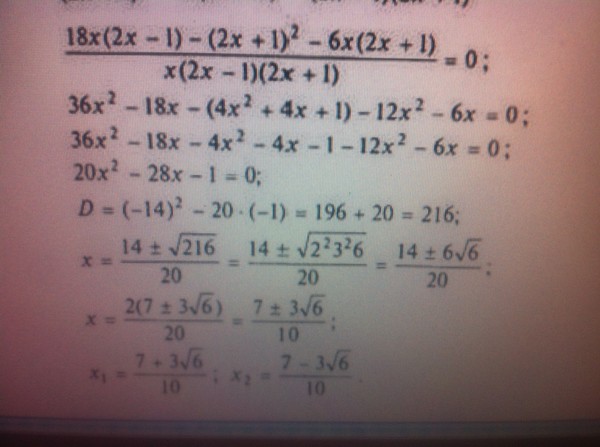
Вот там, где пошло решение через дискриминант, каким образом вышли такие значения? Что там поменяли и как, по какому правилу? Это решебник
Есть стандартное квадратное уравнение вида a*x2 + b*x + c = 0
У тебя в варианте:
20*x2 - 28*x -1 = 0
a*x2 + b*x + c = 0
Значит, a = 20, b = -28, c = -1
Дискриминант вычисляется по формуле:
D = b2 - 4*a*c = (-28)*(-28) - 4*(20)*(-1) = 784 + 80 = 864.
Или, как у вас у уравнении, дискриминант деленный на 4.
D = (b/2)^2 (b пополам в квадрате) - a*c = 196 + 20 = 216.
Дискриминант деленный на 4 целесообразно использовать, если у вас b четное. В любом случае, какой бы вы дискриминант не выбрали, ответ у вас будет одинаково правильный.
P.S.
Ответы у вас верные, но не забудьте написать ОДЗ (область допустимых значений) . Икс не может быть равен 0.5, -0.5 и 0. Так как иначе в знаменателе будет ноль, а на ноль вам ещё рано делить =)
Мозги людям пудрят четными b, вот и все...
Если уравнение имеет вид ах2+2kx+c=0, то можно считать по формуле Х1,2=(-k +V(D/4))/a, где D/4=k2 - ас.
ax^2 + bx + c = 0
x(1,2) = [-b +- V{b^2 - 4ac}] \2a
Пропущена 4 в (-4ac)
20x^2 - 28x - 1 = 0
x(1,2) = [+28 +- V{(-28)^2 - 4*20*(-1)}] \ 2*20 =
= [28 +- V{784 + 80}] \ 40 =
= [28 +- V864] \40 =
= (28 +- V(12*12*6) \ 40 =
= (28 +- 12V6) \ 40 = (7 +- 3V6) \ 10
Здесь всё правильно. 4-ку пропустили, так как это формула Д1=(К в квадрате) -ас, из которой К= половине -28= -14
Это другая формула дискриминанта, применяется, только когда "б"- чётное число, то бишь можно делить на два.
здесь решали другим способом, тоесть не через б, а через к, следовательно формула другая
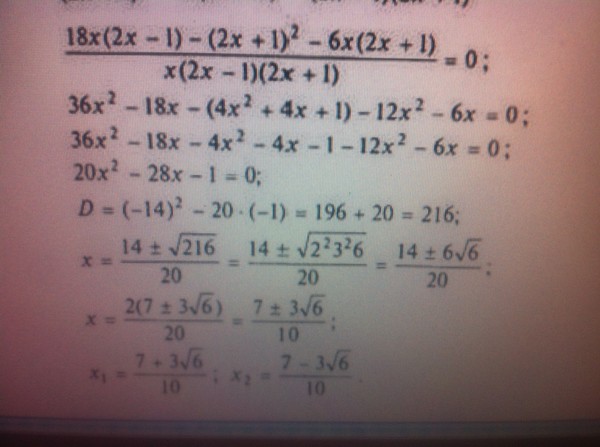
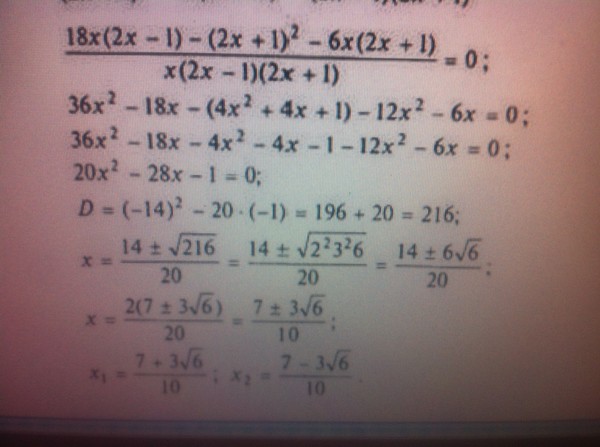
то есть a=20; b=28; c=-1, так?
почему в дискриминанте другие значения стоят?
почему b=-14, а 4-ку, которая идет по формуле вообще пропустили?
хочу понять каким образом