Естественные науки

Как вы считаете можно ли определить широту на которой находится наблюдатель, если замерять время восхода солнца....

и знать при этом, что восход солнца на экваторе длится ровно две минуты?
Как это сделать?
Елена Величко
Елена Величко
75 713
можно, но точность будет очень плохой и нужно вводить поправку от времени года (вблизи полярного круга зимой и летом восход будет очень долгим, если вообще будет)
ВМ
Владимир Мельник
77 820
Лучший ответ
по времени восхода можно оценить долготу, а не широту.
А широту - по высоте подъёма солнца над горизонтом в полдень (истинный, а не по часовому поясу), с учётом даты.
Юлия Галацевич
Юлия Галацевич
50 011
Гаухара Такенова Когда мы отмечаем время восхода Солнца, просто смотрим на часы. Но автор пишет: "...если ЗАМЕРЯТЬ время восхода солнца...". Поэтому я полагал, что автор за словом "время" имел в виду продолжительность восхода - от появления верхнего края Солнца до момента, когда нижний его край оказывается на горизонте. Тем более он (автор) далее пишет о ДЛИТЕЛЬНОСТИ восхода на экваторе (2 мин). Может быть, ошибаюсь - чтО имел в душе автор га самом деле - нам не знать.
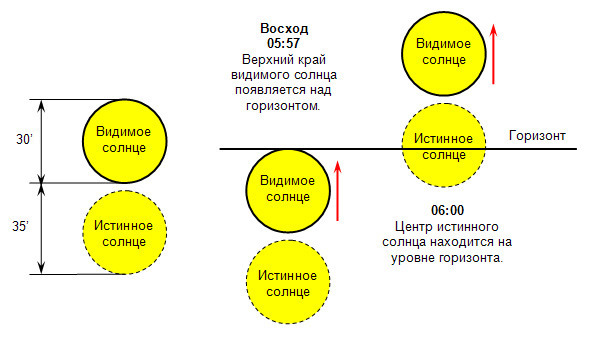
Надо ещё отвлечься от явления рефракции солнечных лучей.
Да, можно определить. Я нашёл ф-лу φ= arccos(2/t), где t - продолжительность восхода Солнца (показался край и взошёл полностью) в данной местности, в мин.
Правда, пока не установил, верна ли ф-ла для любого дня года или только для дней равноденствий. Подумаю ещё (скорее всего для любого времени года).
Самал Мыспаева
Самал Мыспаева
94 250
Самал Мыспаева Да, ф-ла работает в любое время года; лишь бы наблюдался полный восход.
И рефракция тут не причём.
Самал Мыспаева Обратным расчётом можно оценить и продолжительность восхода Солнца.
Например, геогр. широта Москвы φ= 55,75о. Тогда
t= 2/cosφ= 2/cos55,75о= 2/0,5628= 3 мин 33 сек. Разумеется, с минус-плюсом.
Надо еще и высоту подъема солнца учитывать в полдень. Это все прописано в трудах Аристотеля, Евклида, Пифагора, а позже Ньютона и Коперника. Но началось еще со времен создания солнечных часов
АК
Арман Касенов
76 660
См. ответ Рустема Искендерова, но только в равноденствия. Вне равноденствий восход будет дольше, и чем выше широта, тем больше разница. У полярного круга время восхода в летнее и зимнее солнцестояние может составить десятки минут (только летом "восход" будет у полуночи, а зимой - у полудня).
Плюс учитываем погрешность на сплющивающую солнце рефракцию, которая в разные дни над разными поверхностями может отличаться, и небольшую погрешность на угловой диаметр Солнца (около 3% из-за эллиптичности орбиты Земли).
РР
Роман Ромыч
60 120
Самал Мыспаева "Вне равноденствий восход будет дольше, и чем выше широта, тем больше разница". Со 2-й частью этого утверждения полностью согласен. На широте Москвы (φ= 55,75о) этот промежуток времени равен (по "моей" ф-ле) 3 мин 33 с, а на экваторе (φ= 0о) - 2 мин. Но в Москве, благодаря тому, что Солнце пересекает горизонт под углом 90-φ= 34,25о В ЛЮБОЕ ВРЕМЯ года (а не только в дни равноденствий), длительность восхода будет одной и той же: 3 мин 33 с. Правда, с этим процессом не разобрался до конца за полярным кругом, но очевидно, что то же будет иметь место и там везде и всегда, где процесс восхода будет наблюдаться с начала до конца... (Продолж. следует.)
Самал Мыспаева Насчёт рефракции. Благодаря ей начало и конец восхода сместятся вперёд, но примерно на одно и то же значение (ибо угловой размер Солнца незначителен - в полградуса); поэтому и продолжительность восхода почти не изменится из-за рефракции.
Роман Ромыч Солнце вне равноденствий находится на разных небесных параллелях, а они пересекают горизонт (который есть круг) под разным углом с точки зрения наблюдателя. На западе и востоке - под углом 90 град минус широта местности, а на севере и юге касательные к ним параллельны горизонту.
Проверил по Старкалку для Екатеринбурга - 22.12 восход длится 5 мин 35 с (плюс-минус пара секунд), 21.03 - 3 мин. 53 с, 22.06 - 5 мин 38 с. То есть продолжительность восхода еще и более-менее симметрично растет относительно равноденствий, что логично (склонение-то Солнца по модулю одинаково). У полярного круга солнце вообще может в солнцестояние ползти по горизонту долго.
Касательно рефракции - признаю, да, атмосфера "плющит" и солнце, и его скорость движения, так что время восхода не изменится.
Роман Ромыч Хотя локальные эффекты турбулентности, колбасящие солнечный край, могут дать несколько секунд погрешности)
Роман Ромыч Впрочем, это всё в принципе решается для задачи в вопросе, если измерить еще и продолжительность дня и свериться с какой-нибудь таблицей или номограммой.

Похожие вопросы