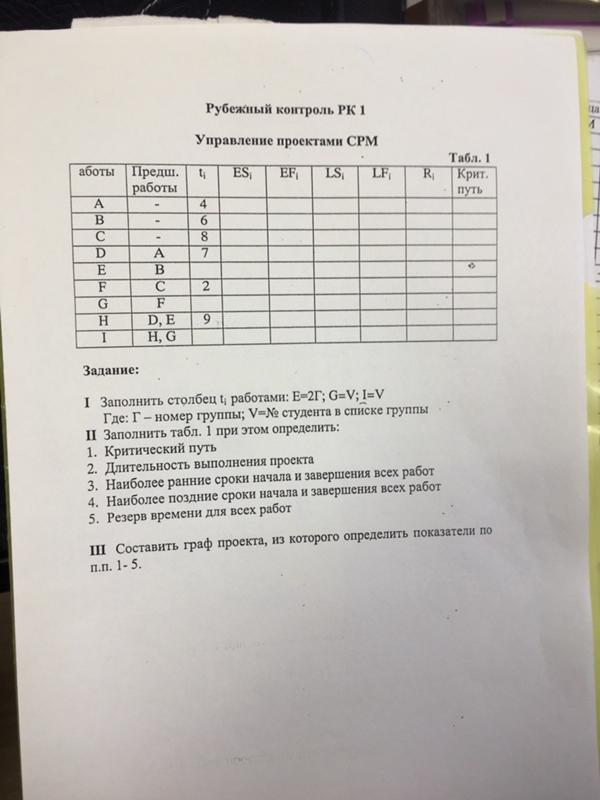
Ребят как найти критический путь: ранние сроки, поздние сроки?

Ну, вычисли по формулам и вставь в таблицу отсутствующие времена работ, потом по таблице взаимозависимости работ и времен их выполнения составь временной сетевой граф. Из его анализа будет сразу виден список критических работ, и некритических тоже. Из этого графа и таблицы взаимозависимости работ легко найти резервы времени для некритических работ.
Минимальные сроки начала и окончания всех работ как раз и отмечаются на временном сетевом графе. У критических работ резервы времени всегда равны нулю, поэтому у них ранние и поздние сроки выполнения работ равны ранним срокам. Для некритических работ поздние сроки начала и окончания работ равны ранним плюс соответствующий резерв времени.

Может это поможет: http://www.studfiles.ru/preview/5006284/page:22/

.

Любая последовательность работ сетевого графика, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы, называется путем.

Путь сетевого графика, в котором начальная точка совпадает с исходным событием, а конечная – с завершающим событием, называется полным.

Путь от исходного события до любого взятого предшествует данному событию. Предшествующий событию путь, имеющий наибольшую длину, называется максимальным предшествующим. Он обозначается L1(i), а его продолжительность t[L1(i)].

Путь, соединяющий любое взятое событие с завершающим, называется последующим путем. Такой путь с наибольшей длиной называется максимально последующим и обозначается L2(i), а его продолжительность t[L2(i)].

Полный путь, имеющий наибольшую длину, называется критическим. Пути, отличные от критического, называются ненапряженными. Они имеют резервы времени.

Работы критического пути выделяются жирными линиями или двойными. Продолжительность критического пути считается главным параметром графика.

Рассмотрим алгоритм определения критического пути на сетевом графике, использующий алгоритм метода динамического программирования.

Упорядочим вершины графика по рангам и пронумеруем их с конца к началу. Это позволит совместить номера рангов с этапами попятного движения при отыскании условно-оптимальных управлений на последнем, двух последних и т. д. этапах. Нахождение критического пути разберем на примере сетевого графика, изображенного на рис. 10.7.