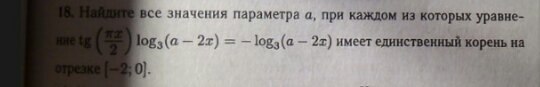
ВУЗы и колледжи
Задание с параметром / ЕГЭ. Помогите решить задачу.
Найти все значения параметра а, при каждом из которых уравнение имеет единственный корень на отрезке [-2;0]
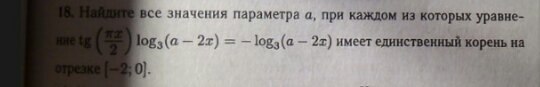
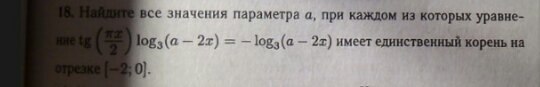
Появилось немного свободного времени. Захотелось решить что-нибудь с параметром, тем более, что решение Володи неправильное. Отдаю себе отчёт в том, что наверняка есть более рациональный способ решения этого уравнения.




Серёга Щукин
Решил задачу графически.




Если условно сократить логарифм (разделить на него обе части), то видим, что корни его получаются из уравнения tg(πx/2) = –1, и на заданном участке [–2;0] корень у него — единственный (Х₁ = –0,5).
Требуется, чтобы на остальной части оси 0Х логарифм МОГ СУЩЕСТВОВАТЬ — чтобы проявился корень Х₁ (Какое у логарифма основание — неважно).
Значит, параметр «а» надо взять таким, чтобы на участке [–2; 0] было: (а – 2x) > 0.
1. a – (–4) > 0 ==> a > – 4.
2. а – 0 > 0 ==> а > 0.
Суммарно: а > 0.
Чтобы второй корень был в интервале [ –2; –0,5], положим: Х₂ = (а – 1)/2 = –2 и = –0,5. А это означает, что при –3 < а < –1 корень Х₁ = –0,5 уже не попадёт в [–2;0], останется только некоторый Х₂.
В итоге, при а > –1 внутри интервала [–2;0] имеем только корень Х₁ = –0,5. { Отвечающий этим «а» корень Х₂ будет больше 0 и не попадёт в [–2; 0].
Однако, при а < –1 корень Х₁ = –0,5 уже отсутствует.
Полный ответ:
На интервале [–2; 0] будет по одному корню при
1) а >= 0;
2) –3 =< а =< –1.
Требуется, чтобы на остальной части оси 0Х логарифм МОГ СУЩЕСТВОВАТЬ — чтобы проявился корень Х₁ (Какое у логарифма основание — неважно).
Значит, параметр «а» надо взять таким, чтобы на участке [–2; 0] было: (а – 2x) > 0.
1. a – (–4) > 0 ==> a > – 4.
2. а – 0 > 0 ==> а > 0.
Суммарно: а > 0.
Чтобы второй корень был в интервале [ –2; –0,5], положим: Х₂ = (а – 1)/2 = –2 и = –0,5. А это означает, что при –3 < а < –1 корень Х₁ = –0,5 уже не попадёт в [–2;0], останется только некоторый Х₂.
В итоге, при а > –1 внутри интервала [–2;0] имеем только корень Х₁ = –0,5. { Отвечающий этим «а» корень Х₂ будет больше 0 и не попадёт в [–2; 0].
Однако, при а < –1 корень Х₁ = –0,5 уже отсутствует.
Полный ответ:
На интервале [–2; 0] будет по одному корню при
1) а >= 0;
2) –3 =< а =< –1.
Похожие вопросы
- помогите решить задачу по физике ЕГЭ
- Помогите решить задачу по экономике организации. Задание: определите рентабельность производственных фондов предприятия
- помогите решить задачи по юриспруденции
- помогите решить задачу по физике срочно пожалуйста
- помогите решить задачу по гражданскому праву
- Помогите решить задачу по теории вероятности
- помогите решить задачи по биологии
- Помогите решить задачу
- Добрый день. Помогите решить задачу из контрольной по высшей математике.
- Помогите решить задачу на ассемблере


