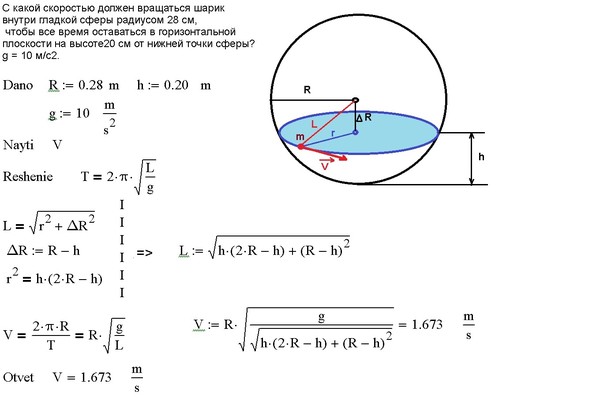
С какой скоростью должен вращаться шарик внутри гладкой сферы радиусом 28 см,

.. |>
.. |)
.. |)
\=|-__7
Zhelayu uspekhov !!!
Vladimir Shchookin.

Имеем: w^2r= g/tga, где r= Rcosa, a - угол "радиус-вектора" шарика относительно горизонта. Отсюда w= sqrt(g/(Rsina)); но Rsina= R-h. Следовательно, w= sqrt(g/(R-h))= sqrt(1000/(28-20))= 5sqrt(5) paд/c= 106,8 oб/мин.

на шарик действуют три силы: сила тяжести mg, направленная вертикально вниз, центробежная сила mV^2/r, направленная горизонтально и сила реакции сферы N, направленная к центру сферы. разложим последнюю силу на две составляющие - вертикальную Nsina и горизонтальную Ncosa, гре а - угол между радиусом вращения шарика r и радиусом сферы R проведенным в точку нахождения шарика. уравнения равновесия шарика по осям будут: mV^2/r=Ncosa, mg=Nsina. разделим первое на второе, получаем V^2/2g=ctga, но ctga=r/(R-h), а r=(R^2-(R-h)^2)^1/2. собирая все в кучу получаем V=(2g(Rh-h^2)/(R-h))^1/2=8,19м/с

на шарик действуют три силы: сила тяжести mg, направленная вертикально вниз, центробежная сила mV^2/r, направленная горизонтально и сила реакции сферы N, направленная к центру сферы. разложим последнюю силу на две составляющие - вертикальную Nsina и горизонтальную Ncosa, где а - угол между радиусом вращения шарика r и радиусом сферы R проведенным в точку нахождения шарика. уравнения равновесия шарика по осям будут: mV^2/r=Ncosa, mg=Nsina. разделим первое на второе, получаем V^2/rg=ctga, но ctga=r/(R-h), а r=(R^2-(R-h)^2)^1/2. собирая все в кучу получаем v=(r^2*g/(R-h))^1/2=3 м/с

Решение не верное, хоть ты и просветленный. Ведь L это радиус сферы R. Ответ должен быть 3 м/с

Вы не учитываете силу трения которая способствует удерживаться телу на одном уровне в сфере. Без нее тело бы просто улетало в бесконечность или наоборот лежало неподвижно на дне сферы как бы вы ее не крутили. Это обычная задача из динамики, хотя и считается что эта тема в динамике является самой сложной.