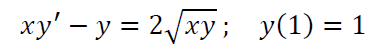 Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.
Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.
Прочее образование
Математика, высшая математика, проблемы с заданием
В общем я второкурсник. У нас есть дисциплина численные методы. И вот в предпоследней работе мне встречается это. Я прошерстил весь интернет, всё и вся лекций преподавателя, нет подсказки или алгоритма решения этого. ПРОШУ ПАМАГИТЕ, хоть ссылкой хоть намёком, куда итди и чо с этим делать. Это единственное задание которое ну не даётся. А не сдать нельзя, надо чтоб все задания были сделаны. Заранее спасибо. 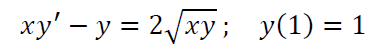 Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.
Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.
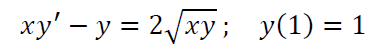 Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.
Просьба тех кто думает что я халявщик просто пройти мимо, это реально сложное задание.Задача представляет собой первоначальную краевую задачу для обыкновенного дифференциального уравнения (ОДУ). В данном случае, уравнение имеет вид:
xy' - y = 2√(xy)
с начальным условием y(1) = 1.
Для решения этого уравнения мы можем попробовать метод разделения переменных. Начнем с переписывания уравнения в виде:
y' - (1/x)y = 2√(x)
Теперь предположим, что решение имеет вид y(x) = x * v(x), где v(x) - некоторая функция x. Тогда, y'(x) = v(x) + x * v'(x). Заменим y и y' в исходном уравнении:
x(v + xv') - xv = 2√(x^2 * v)
упрощаем:
xv' = 2√(x^2 * v)
Теперь разделим переменные:
v' / (2√v) = 1/x
Интегрируем обе стороны:
∫(dv / (2√v)) = ∫(dx / x)
Получаем:
√v = ln(x) + C
где C - константа интегрирования. Возводим обе стороны в квадрат:
v = (ln(x) + C)^2
Таким образом, решение имеет вид:
y(x) = x * (ln(x) + C)^2
Теперь используем начальное условие y(1) = 1:
1 = 1 * (ln(1) + C)^2
Так как ln(1) = 0, получаем C = 1, и окончательное решение имеет вид:
y(x) = x * (ln(x) + 1)^2
xy' - y = 2√(xy)
с начальным условием y(1) = 1.
Для решения этого уравнения мы можем попробовать метод разделения переменных. Начнем с переписывания уравнения в виде:
y' - (1/x)y = 2√(x)
Теперь предположим, что решение имеет вид y(x) = x * v(x), где v(x) - некоторая функция x. Тогда, y'(x) = v(x) + x * v'(x). Заменим y и y' в исходном уравнении:
x(v + xv') - xv = 2√(x^2 * v)
упрощаем:
xv' = 2√(x^2 * v)
Теперь разделим переменные:
v' / (2√v) = 1/x
Интегрируем обе стороны:
∫(dv / (2√v)) = ∫(dx / x)
Получаем:
√v = ln(x) + C
где C - константа интегрирования. Возводим обе стороны в квадрат:
v = (ln(x) + C)^2
Таким образом, решение имеет вид:
y(x) = x * (ln(x) + C)^2
Теперь используем начальное условие y(1) = 1:
1 = 1 * (ln(1) + C)^2
Так как ln(1) = 0, получаем C = 1, и окончательное решение имеет вид:
y(x) = x * (ln(x) + 1)^2
Сахиб Абдуллаев
спасибо за ответ, но к сожалению таким методом нельзя мне писать, почему то. Типа задание такое. Ещё раз спасибо
Это называется дифференциальным уравнением.
По сути, вам нужно найти функцию y, для которой справедливо указанное равенство.
Я уже сам не помню, как их решать: мне это не пригодилось в жизни.
Но теперь вы знаете, что нужно гуглить.
По сути, вам нужно найти функцию y, для которой справедливо указанное равенство.
Я уже сам не помню, как их решать: мне это не пригодилось в жизни.
Но теперь вы знаете, что нужно гуглить.
Сахиб Абдуллаев
Ну я это знал, поверьте это не просто уравнение, я решил краевую а это никак. из- за корня, что делает стандартные подстановки невозможными. Но за ответ спасибо.
я тоже на втором курсе и я ненавижу высшую математику
попробуй спросить у одноклассников
попробуй спросить у одноклассников
Похожие вопросы
- Высшая математика Вопрос по данному заданию
- Можно ли учить высшую математику, не зная школьного курса? Подробнее внутри
- Где нужна высшая математика кроме программирования?
- Задание из высшей математике.
- Высшая математика задание
- Высшая математика. Теория вероятности
- Математика и высшая математика
- Зачем школьная система России заставляет учить высшую математику?
- 26 баллов по математике, это сколько заданий???
- Зачем изучать высшую математику если давно написаны разные программы для вычислений?



