Реши уравнение, используя введение нового неизвестного:. а)4(x^2-x)^2+9(x^2-x)+2=0 b)x^2-6|x|+5=0

а) 4(x² - x)² + 9(x² - x) + 2 = 0
1) Замена: x² - x = t
4t² + 9t + 2 = 0
D = 81 - 4*4*2 = 49
t₁ = (-9 + 7) / 8 = -0,25
t₂ = (-9 - 7) / 8 = -2
2) Ворачиваемся к замене:
x² - x = -2
x² - x + 2 = 0 - нет действительных корней

x² - x = -0,25
x² - x + 0,25 = 0
(x - 0,5)² = 0
x = 0,5
Ответ: 0,5

б) x² - 6|x| + 5 = 0
Здесь нужно рассматривать два случая:
1) Если x ≥ 0, то x² - 6|x| + 5 = x² - 6x + 5
x² - 6x + 5 = 0
x₁ = 1 - корень
x₂ = 5 - корень
То есть оба эти корни нам подходят, так как они больше нуля.

2) Если x < 0, то x² - 6|x| + 5 = x² - 6(-x) + 5 = 0
x² + 6x + 5 = 0
x₁ = -5 - корень
x₂ = -1 - корень
То есть оба эти корня нам подходят, так как они меньше нуля.

Ответ: 1; 5; -1; -5.

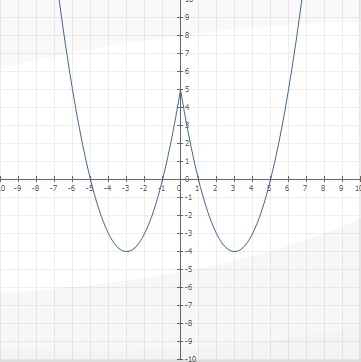
А вот, если интересно, график функции y = x² - 6|x| + 5 = 0. Таким образом, его можно легко решить функционально-графическим методом!

x²-6|x|+5=0 <=> |x|²-6|x|+5=0 <=> (|x|-5)(|x|-1)=0
|x|=5 <=> x=±5, |x|=1 <=> x=±1
Ответ: {±1;±5}.

4((x²-x)+2)((x²-x)+1/4)=0
(x²-x+2)(x²-x+1/4)=0
x²-x+2=0
D< 0, действительных корней нет
x²-x+1/4=0
4x²-4x+1=0
(2x-1)²=0 <=> x=1/2 - корень кратности 2.
Ответ: 1/2.

замените x^2-x=а
и решайте
4a^2+9a+2=0
потом получите а подставьте в 1 выражение и решите уще одно уравнение

а второе модуль х заменпите на а, учитывая, что модуль х в квадрате и х в квадрате равны
решайте a^2-6a+5=0
это даже помогу вам: a=5 или а=1
а т. к. модуль х равно а, то х=5,-5,1,-1
вот и всё

а) х=1/2
б) х=1,х=5; x=-1,x=-5