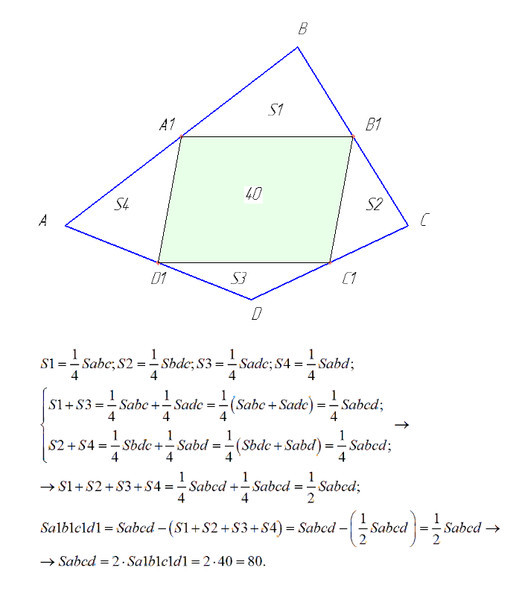
S четырёхуг, вершинами которого служат середины сторон выпуклого четырёхуг ABCD, равна 40 см². Найти S четырёхуг ABCD.

P.S. Для nastya dementeva:

А в чем смысл копирования и выкладвывания чужих ответов ?

S = s + (ав sin А+вс sin B + cd sin C + ad sin D)/8 = (ав sin A + cd sin C)/2 = (bc sin B +ad sin D)/2 =
= s + (S/4) + (S/4) = s + (S/2) = S

то есть S = 2s

Здесь записано, что площадь четырехугольника АВСD равна:

маленький четырехугольник с площадью s + сумма площадей оставшихся треугольничков, которые определялись по формуле:
площадь треугольника (вроде) равна произведению сторон на синус угла между ними и разделить пополам.

также площадь АВСD просто равна сумме площадей двух треугольников, которые получаются при проведении диагоналей (две диагонали - две формулы записаны соответственно) , тоже через стороны и синус угла между ними.

здесь между сторонами а, в угол А,
между сторонами в, с угол В,
между сторонами с, d угол С,
между сторонами a, d угол D.
в маленьких треугольничках, соответствующие стороны равны а/2, в/2, с/2, d/2 ))

S = s + (ав sin А+вс sin B + cd sin C + ad sin D)/8 = (ав sin A + cd sin C)/2 = (bc sin B +ad sin D)/2 = = s + (S/4) + (S/4) = s + (S/2) = Sто есть S = 2sЗдесь записано, что площадь четырехугольника АВСD равна: маленький четырехугольник с площадью s + сумма площадей оставшихся треугольничков, которые определялись по формуле: площадь треугольника (вроде) равна произведению сторон на синус угла между ними и разделить пополам. также площадь АВСD просто равна сумме площадей двух треугольников, которые получаются при проведении диагоналей (две диагонали - две формулы записаны соответственно) , тоже через стороны и синус угла между ними. здесь между сторонами а, в угол А, между сторонами в, с угол В, между сторонами с, d угол С, между сторонами a, d угол D. в маленьких треугольничках, соответствующие стороны равны а/2, в/2, с/2, d/2 ))