Графы. Как доказать?:
1)Пусть в полном графе степень каждой вершины равна deg v=3 и длина минимального цикла l=5. Показать, что в таком графе по крайней мере 20 вершин.
2) Что если q>(p-1)(p-2)/2, то граф связный.
3)задача с графом Дано корневое дерево с k висячими вершинами, нет вершин степени 2, отличных от корня. Доказать , что при k>=2 общее число вершин не превосходит 2k-1
4)решить задачку про то что 2 графа с неболее 4 вершин, и одинаковыми степенями вершин изоморфны
ВУЗы и колледжи
Графы. Как доказать?
Например, первая задача.
Полный граф, имеющий степень каждой вершины deg v = 3 — тетраэдр. Но у тетраэдра длина минимального цикла равна трём. Похоже, имеется ввиду планарный граф. По теореме Эйлера можно показать, что это планарный граф додекаэдра:
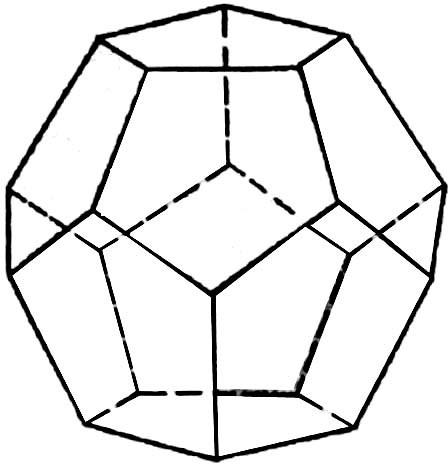
Если в графе все циклы минимальной длины 5, то по т. Эйлера: V − R + G = 2, где
V — число вершин
R — число рёбер
G — число граней
С учётом соотношения 3V = 2R (сумма степеней вершин равна удвоенному числу рёбер) .
В частности 2R = 5G ⇔ G = 3V/5. Имеем следующее уравнение:
V − 3V/2 + 3V/5 = 2 ⇔ V = 20.
Если полагать, что есть грани с длиной цикла более 5, то G = 3V/c < 3V/5, где с > 5 — а это уже большее значение корня для V в силу линейности по V. То есть, V = 20 — минимальное возможное значение.
Полный граф, имеющий степень каждой вершины deg v = 3 — тетраэдр. Но у тетраэдра длина минимального цикла равна трём. Похоже, имеется ввиду планарный граф. По теореме Эйлера можно показать, что это планарный граф додекаэдра:

Если в графе все циклы минимальной длины 5, то по т. Эйлера: V − R + G = 2, где
V — число вершин
R — число рёбер
G — число граней
С учётом соотношения 3V = 2R (сумма степеней вершин равна удвоенному числу рёбер) .
В частности 2R = 5G ⇔ G = 3V/5. Имеем следующее уравнение:
V − 3V/2 + 3V/5 = 2 ⇔ V = 20.
Если полагать, что есть грани с длиной цикла более 5, то G = 3V/c < 3V/5, где с > 5 — а это уже большее значение корня для V в силу линейности по V. То есть, V = 20 — минимальное возможное значение.
1) лемма о рукопожатиях, 3п = 2ку. Теорема о связи числа ребер и длинны минимального цикла. Имеем п >= 20.
2) теорема о количестве ребер и следствие из нее
3) индукция. Бери самое маленькое дерево в базу, и шаги - 2 поддерева + новый корень
4) перебрать их все )
2) теорема о количестве ребер и следствие из нее
3) индукция. Бери самое маленькое дерево в базу, и шаги - 2 поддерева + новый корень
4) перебрать их все )
Похожие вопросы
- 1) Доказать тождество: A и (B ∆ C) = (A и B) ∆ (A и C). (показать решение на кругах Эйлера) 2) Доказать, что: A
- Помогите доказать, пожалуйста.
- Хроматический полином графа. Как его найти и что это вообще такое???
- куда поступать?закончила худ.школу документы подаю на худ.граф.(модельер)и на экспертизу недвижимости!что выбрать?
- Как доказать это неравенство с помощью математической индукции?
- Доказать что в своих стихах некрасов пишет про себя. Доказать что в своих стихах некрасов пишет про себя
- Доказать что прямая параллельна плоскости, а другая прямая лежит в этой плоскости
- «Конституция» графа М. Лорис-Меликова мне нужен реферат на эту тему
- Как доказать логическую задачу?
- Докажите истинность тезиса апагогическим способом (методом «от противного»):

