ВУЗы и колледжи
Какие функции называются периодическими? Примеры
Функция, ее свойства и графики
Основное свойство периодической функции - и оно же ее определение:
f(x)=f(x+T)=f(x+n*T)
где x - переменная
T - период функции, т. е. такой отрезок по оси х, где значение функции повторяеться,
n - целое число, 0,1,2....-1, -2, -3 ...
Особенность такой функции - достаточно построить график в предалах одного периода (исследовать ее там) - а потом просто копировать его в обе строны
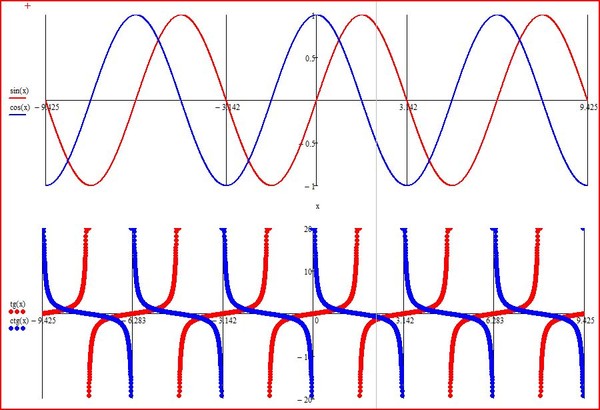
Примеры: функция синуса и косинуса - период 2 пи, а также тангенса и котангенса - период пи (черными вертикалями выдеоин один период, их в принципе можно произвольни сдвигать - но только вместе! )
f(x)=f(x+T)=f(x+n*T)
где x - переменная
T - период функции, т. е. такой отрезок по оси х, где значение функции повторяеться,
n - целое число, 0,1,2....-1, -2, -3 ...
Особенность такой функции - достаточно построить график в предалах одного периода (исследовать ее там) - а потом просто копировать его в обе строны
Примеры: функция синуса и косинуса - период 2 пи, а также тангенса и котангенса - период пи (черными вертикалями выдеоин один период, их в принципе можно произвольни сдвигать - но только вместе! )

Функцию называют периодической, если она имеет период (хотя бы один) .
Периодические функции возникают при описании колебательных процессов.
http://nature.web.ru/db/msg.html?mid=1158396&uri=s2node4.html
Функция f (x), определенная на числовом множестве X, называется периодической, если существует такое число w? 0, называемое периодом, что для любого x k X выполняются условия
x + w k X, x - w k X ;
f (x + w) = f (x), f (x - w) = f (x).
http://www.pereplet.ru/obrazovanie/stsoros/969.html
Функция у = f(x) называется периодической, если существует число такое, что для каждого значения аргумента х из области ее значения имеет место равенство
Число Т называют периодом функции.
Из определения следует, что числа (k = 0,±1,±2,...) также являются периодами.
Наименьший положительный период, если он существует, называется основным периодом.
http://school-collection.edu.ru/catalog/res/a25f5ab8-fee7-e49f-e471-b0b69866d822/view/.
Функция f(х) называется периодической функцией, если существует число Т, такое, что выполняются условия:
если x Î D(f), то x + T Î D(f) и x – T Î D(f)
для любого x Î D(f), f(x+T) = f(x).
Наименьшее положительное число Т, удовлетворяющее этим условиям, называется периодом функции.
http://sferica.by.ru/lessons/alg10_1.html
Функция, определенная на множестве, называется периодической, если существует число такое, а) что для любого значения и тоже принадлежат ; б) . Число при этом называют периодом функции.
Если функция периодическая на множестве и на, то для нее существует наименьший положительный период и любой период этой функции имеет вид, где . называют основным периодом функции .
http://pakhomova.tpu.ru/IMO_Math_analysis-01/Lectures/Lecture-01.doc.
Периодические функции возникают при описании колебательных процессов.
http://nature.web.ru/db/msg.html?mid=1158396&uri=s2node4.html
Функция f (x), определенная на числовом множестве X, называется периодической, если существует такое число w? 0, называемое периодом, что для любого x k X выполняются условия
x + w k X, x - w k X ;
f (x + w) = f (x), f (x - w) = f (x).
http://www.pereplet.ru/obrazovanie/stsoros/969.html
Функция у = f(x) называется периодической, если существует число такое, что для каждого значения аргумента х из области ее значения имеет место равенство
Число Т называют периодом функции.
Из определения следует, что числа (k = 0,±1,±2,...) также являются периодами.
Наименьший положительный период, если он существует, называется основным периодом.
http://school-collection.edu.ru/catalog/res/a25f5ab8-fee7-e49f-e471-b0b69866d822/view/.
Функция f(х) называется периодической функцией, если существует число Т, такое, что выполняются условия:
если x Î D(f), то x + T Î D(f) и x – T Î D(f)
для любого x Î D(f), f(x+T) = f(x).
Наименьшее положительное число Т, удовлетворяющее этим условиям, называется периодом функции.
http://sferica.by.ru/lessons/alg10_1.html
Функция, определенная на множестве, называется периодической, если существует число такое, а) что для любого значения и тоже принадлежат ; б) . Число при этом называют периодом функции.
Если функция периодическая на множестве и на, то для нее существует наименьший положительный период и любой период этой функции имеет вид, где . называют основным периодом функции .
http://pakhomova.tpu.ru/IMO_Math_analysis-01/Lectures/Lecture-01.doc.
например f(x)=[x] или f(x)={x} Функция целая чась, функция дробная часть
Это такие функции, значение которых повторяется через определённый интервал изменения аргумента. Например, синус, косинус. Т. е. , sin(0) = sin(2pi) = sin(4pi) = 0, или cos(1/2pi) = cos(5/2pi) = cos(9/2pi) = 1.
Похожие вопросы
- Какая функция называется функцией двух переменных?
- Расскажите пожалуйста об основных функциях денег. Приведите примеры
- подскажите свойства функции Y = ctgX. пожаалуйста без числовых примеров. просто общие свойства. заранее спасибо)
- Высшая математика Исследовать свойства функции и построить график. y(x)=x^4 - 2x^2 + 3(если что фото в описании)
- Считаете ли вы необходимой периодическую аттестацию научных кадров?
- По положению атома элемента в Периодической системе...
- На рынке совершенной конкуренции функция рыночного спроса имеет вид: Р
- помогите исследовать функцию y = x^2*e^-x по схеме
- Алгебра....помогите исследовать функцию
- Производственная функция Кобба-Дугласа.



