Помогите ПОЖАЛУЙСТА
решить уравнение модуль в модуле и квадрат внутри. |x^2 + |X-5||=7
ВУЗы и колледжи
Помогите ПОЖАЛУЙСТА решить уравнение модуль в модуле и квадрат внутри. |x^2 + |X-5||=7
|x² + |x-5||=7 <=> x² + |x-5|=7 - сумма положительных чисел, 7-x²≥0,-√7 ≤x≤√7, <=> √(x-5)²=7-x² - свойство модуля
√(x-5)²=7-x², ->(x-5)²=(7-x²)², (x-5-7+x²)(x-5+7-x²)=(x²+x-12)(-x²+x+2)=0,
x²+x-12=0, x1=-4, x2=3 - т. Виета - оба корня посторонних, т. к не удовл. ОДЗ
-x²+x+2=0, x²-x-2=0, x1=-1, x2=2 - т. Виета, удовл. ОДЗ
Графическое решение:
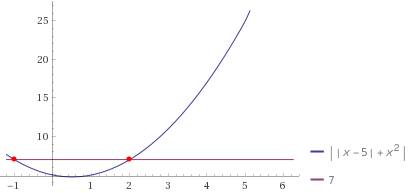
√(x-5)²=7-x², ->(x-5)²=(7-x²)², (x-5-7+x²)(x-5+7-x²)=(x²+x-12)(-x²+x+2)=0,
x²+x-12=0, x1=-4, x2=3 - т. Виета - оба корня посторонних, т. к не удовл. ОДЗ
-x²+x+2=0, x²-x-2=0, x1=-1, x2=2 - т. Виета, удовл. ОДЗ
Графическое решение:

Кенжегуль Рамазанова
Это просто отлично. Но не поняла, почему первая скобка должна удовлетворять условию х >5, а вторая х <5?
Дамир Глямшин
x1=-1, x2=-2 - т. Виета не выполняется, надо х1=-1 х2=2
Кенжегуль Рамазанова
А какое здесь ОДЗ????
Внешний модуль можно вообще откинуть, так как там всегда сумма двух положительных чисел. Задача сводится к решению 2-х обычных уравнений: 1-е это для x>5 ---> x^2+x-5=7 --> x1=3 x2=-4 Оба корня не подходят. 2- уравнение для x<5 ---< x^2-x+5=7 ---> x1=2 x2=-1 Оба корня подходят
Кенжегуль Рамазанова
Благодарю!
1) x^2 + x - 12 = 0
2) x^2 - x - 2 = 0
3) x^2 + x - 2 = 0
4) x^2 - x + 12 = 0
1) D = 1 + 48 = 49
x1 = -1 - 7 /2 = -8/2 = -4
x2 = -1 + 7 /2 = 6/2 = 3
2)D = 1 + 8 = 9
x1 = 1 - 3 / 2 = -2/2 = -1
x2 = 4/2 = 2
3) D = 9
x1 = -1 -3 / 2 = -4/2 = -2
x2 = -1 + 3/2 = 1
4) D<0
Ответ: х = 2, х = -1, х = 3, х = -4
2) x^2 - x - 2 = 0
3) x^2 + x - 2 = 0
4) x^2 - x + 12 = 0
1) D = 1 + 48 = 49
x1 = -1 - 7 /2 = -8/2 = -4
x2 = -1 + 7 /2 = 6/2 = 3
2)D = 1 + 8 = 9
x1 = 1 - 3 / 2 = -2/2 = -1
x2 = 4/2 = 2
3) D = 9
x1 = -1 -3 / 2 = -4/2 = -2
x2 = -1 + 3/2 = 1
4) D<0
Ответ: х = 2, х = -1, х = 3, х = -4
Кенжегуль Рамазанова
Спасибо огромное, я думала решаю неправильно. Только у меня в пункте 3) x^2 +x+2 =0
Маришка ***
Подставь в исходное уравнение х=3 и х=4 и увидишь, что они не подходят
Елена Бычковская
Полная чушь.
Ольга Тамкович
Подставь свой результат в исходное и посмеемся вместе.
Похожие вопросы
- помогите пожалуйста решить уравнение ЛНДУ: 1)y''-3y'+2y=cos x И найти производную (1 и 2) y= (Ax+B)cos2x+(Cx+D)sin2x
- помогите пожалуйста решить а (log7(|x|+7) - a - 2)корень (log 7(|x|+7)=0
- Помогите,пожалуйста,решить уравнение!!!Срочно!!!!4sin(5pi/2-4x)+4sin(6pi+2x)=1
- Помогите, пожалуйста решить уравнения из теории комплексного анализа, пожалуйста
- помогите решить алгебру....1} 5-3(x-2(x-2(x-2)))=2 2} корень из 2х-1= x-2 3} (x+5)/-3>(5x-1)/4
- Помогите пожалуйста. Нужно найти уравнения касательных к параболе y^2=20\3*x и элипсу x^2\45+y^2\20=1.
- Помогите плз с задачами: Показать что ф-ция z=ln(y^2+x^2) удовлетворяет уравнению 1/x*dz/dx+1/y*dz/dy=z/(y^2)
- -x^2+2x-5=0 имеет ли корни? Подскажите пожалуйста
- решите пжл интеграл) ) xdx/(x+2)(x^2+4x+5) (спасибо)
- Помогите пожалуйста решить 7 примеров lim


