Решить дифференциальные уравнения.

Ответ. 3*y'-(y^2)/(x^2)-(8*y)/x-4=0; y'+y/x-sin(x)=0; 2*x*y*y'-y'^2-1=0;

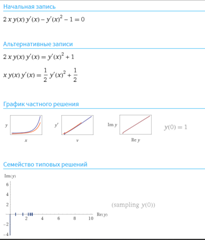
2) 3y' = (y/x)^2 +8*(y/x) + 4 - это однородное ДУ
Делаем замену z = y/x => y' = z + x*z'
=> 3*(z + x*z') = z^2 + 8z + 4 - это ДУ с разделяющимися переменными
3x*z' = z^2 + 5z + 4
=> dz/[(z+4)*(z+1)] = dx/(3x)
=> (1/3)*[dz/(z+1) - dz/(z+4)] = dx/(3x)
=> ln|z+1| - ln|z+4| = ln|x| + ln|C|
=> z+1 = C*x*(z+4)
=> z = (4*C*x - 1)/(1-C*x)
z = y/x => y = x*z = [x*(4*C*x-1)]/(1-C*x) - общее решение,
где C - константа.

3) y' + (y/x) = sinx - линейное неоднородное ДУ. Решаем методом Бернулли. Пусть y = u*v =>
=> u'*v + u*v' + u*v/x = sinx
=> u*(v' + v/x) + u'*v = sinx
Функцию v выберем из условия
v' + (v/x) = 0
=> dv/v = -dx/x => v = 1/x
Тогда на u будет ДУ:
u'*v = sinx
=> u' = x*sinx
=> du = -x*dcosx
=> u = -x*cosx + sinx + C
=> y = u*v = (-x*cosx + sinx + C)*(1/x) = (C/x) + (sinx-x*cosx)/x - общее решение, C - константа.

4) 2*x*y'*y'' = (y')^2 + 1
Заменой y' = z понизим порядок:
2*x*z*z' = z^2 + 1 - видим, что имеем ДУ с разделяющимися переменными.
[z/(z^2+1)]dz = dx/(2x)
=>(1/2)*d(z^2+1)/(z^2+1) = dx/(2x)
=> ln(z^2+1) = ln|x| + ln|C1|
=> z^2 + 1 = C1*x
Отсюда две ветки решений:
z = -(C1*x - 1)^(1/2) и z = (C1*x-1)^(1/2)
Вспоминаем, что z = y'
=> y = -[(2/3)*(C1*x-1)^(3/2)]/C1 + C2 и y = [(2/3)*(C1*x-1)^(3/2)]/C1 + C2 - решения,
где C1, C2 - константы