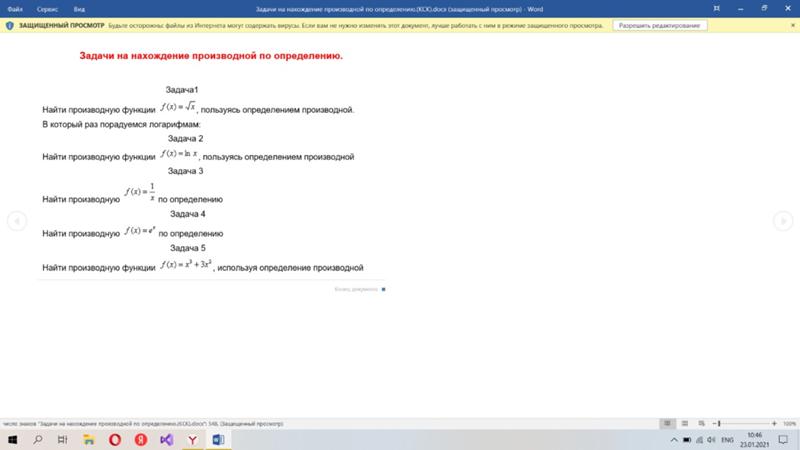
Задачи на нахождение производной

3) f(x)=1/x
x- x0= ∆x, x=x0 +∆x

∆f= f(x0 +∆x) - f(x0)= 1/(x0 +∆x) - 1/x0= ( x0 - x0 - ∆x) / x0(x0 +∆x) = - ∆x / x0(x0 +∆x)

∆f/ ∆x= ( - ∆x / x0(x0 +∆x)) /∆x=( - ∆x / ∆x*x0(x0 +∆x))= -1/ (x0(x0 +∆x));

lim(∆x--->0) ∆f/ ∆x = lim(∆x--->0)( -1/ (x0(x0 +∆x))) = -1/(x0)^2 = >

(1/x)'= - 1/x^2

1) f(x) = √x
∆f= f(x0 +∆x) - f(x0)=√(x0+∆x) - √x0 =

( √(x0+∆x) - √x0 )*( √(x0+∆x) +√x0 ) / ( √(x0+∆x) +√x0 )=

(x0+∆x - x0 )/ ( √(x0+∆x) +√x0 )=

∆x/ ( √(x0+∆x) +√x0 );

∆f/ ∆x=∆x/( ∆x( √(x0+∆x) +√x0 ))= 1/( √(x0+∆x) +√x0 );

lim(∆x--->0) ∆f/ ∆x = lim(∆x--->0) (1/( √(x0+∆x) +√x0 ))= 1/ 2√x0 = >

(√x)' = 1/2√x

=1/(2√x)
=1/x
= -1/(x^2)
=e^x
=3x^2 +6x

Как находить производные по определению:
По определению производной функции f(x) является предел отношения приращения функции к приращению аргумента, то есть в виде формулы:
f'(x) = lim((f(x + dx) - f(x))/dx)
при dx ->0
Рассмотрим пример 1.
f(x) = √(x)
Найдем производную:
lim((√(x + dx) - √(x))/dx) = (1)
фактически нам надо найти предел при dx -> 0
Для этого выражение под пределом умножим и разделим на выражение:
√(x + dx) + √(x)
тогда получим следующий предел:
(1) = lim((x + dx - x)/dx(√(x + dx) + √(x))) = lim(1/(√(x + dx) + √(x)) = устремим dx к 0 = 1/2√(x)
Итого мы получаем значение производной:
d√(x)/dx = 1/2√(x)
Ну и еще пример 2:
Производная от ln(x)
dln(x)/dx = lim((ln(x + dx) - ln(x))/dx) = lim(ln((x + dx)/x)/dx) = (1)
´Преобразуем дробь под логарифмом: x + dx/x = 1 + dx/x
(1) = lim((1/dx)ln(1 + dx/x)) = (2)
умножим и разделим выражение под пределом на х.
(1/x)(x/dx)ln(1 + dx/x) = (1/x)ln(1 + dx/x)^(x/dx)
т. к. 1/x можно вынести из под знака предела, то:
(2) = (1/x)lim(ln(1 + dx/x)^(dx/x)) = (3)
Обозначим y = x/dx
при dx -> 0 x/dx стремится к бесконечности
(3) = (1/x)lim(ln(1 + 1/t)^t = устремляя t в бесконечность получим = (1/x)lim(ln(e)) = 1/x
Итого производная:
dln(x)/dx = 1/x
Аналогично решаются все остальные примеры.
Успехов
(