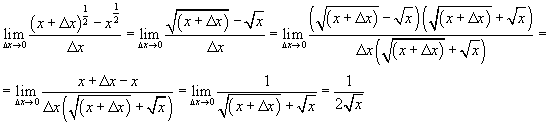
помогите пожалуйста с решением.

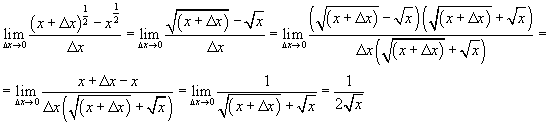
((X + дельта X)^(1/2) - (X)^(1/2)) / дельта Xэ

Если вспомнить определение производной:
f'(x) = (f(x+dx) - f(x))/dx

f(x) = x^0,5
f'(x) = -0,5*x^(-0,5) = 1/(2*x^0,5) (используя правило: f=x^a, F = (x^(a+1))/(a+1))
Если подходить к делу с этой точки зрения =)

если с лимитов.. .
((X+dX)^0,5 - X^0,5) / dX =
Домножаем числитель и знаменатель на такую бяку, чтобы разность квадратов в числителе была) , т. е. на ((X+dX)^0,5 + X^0,5)
= (((X+dX)^0,5 - X^0,5)*((X+dX)^0,5 + X^0,5)) / (dX*((X+dX)^0,5 + X^0,5))
Пользуемся формулой "разность квадратов": ((X+dX)^0,5 - X^0,5)*((X+dX)^0,5 + X^0,5) = X + dX - X = dX
= dX / (dX*((X+dX)^0,5 + X^0,5))
Сокращаем dX:
= 1 / ((X+dX)^0,5 + X^0,5)
Теперь можем принять dX = 0 (предел)
= 1 / (X^0,5 + X^0,5) = 1 / (2*X^0,5)

Всё =)

lim(дельта X стремится к нулю ) ( (X + дельта X)^(1/2) - (X)^(1/2) ) / дельта X = | домножаем на выражение, сопряженное числителю|=
= lim(дельта X стремится к нулю ) ( (X + дельта X)^(1/2) - (X)^(1/2) )*(X + дельта X)^(1/2) + (X)^(1/2) ) / (дельта X.*(X + дельта X)^(1/2) +(X)^(1/2) ) = lim(дельта X стремится к нулю ) ( X + дельта X- X )/ (дельта X.*(X + дельта X)^(1/2) +(X)^(1/2) )= lim(дельта X стремится к нулю ) (дельта X)/ (дельта X.*(X + дельта X)^(1/2) +(X)^(1/2) )=| сокращаем|= lim(дельта X стремится к нулю ) (1/ (X + дельта X)^(1/2) + (X)^(1/2) )=1/ ((x+0) ^(1/2)+(x)^(1/2))=1/(2*x^(1/2))=1/(2*(x)^(1/2) )

* - умножение.

тебе делать нечего в такое время задачки решатиь