Домашние задания: Геометрия
Здравствуйте, прошу добрых людей. Найдите длину общей гипотенузы двух прямоугольных треугольника
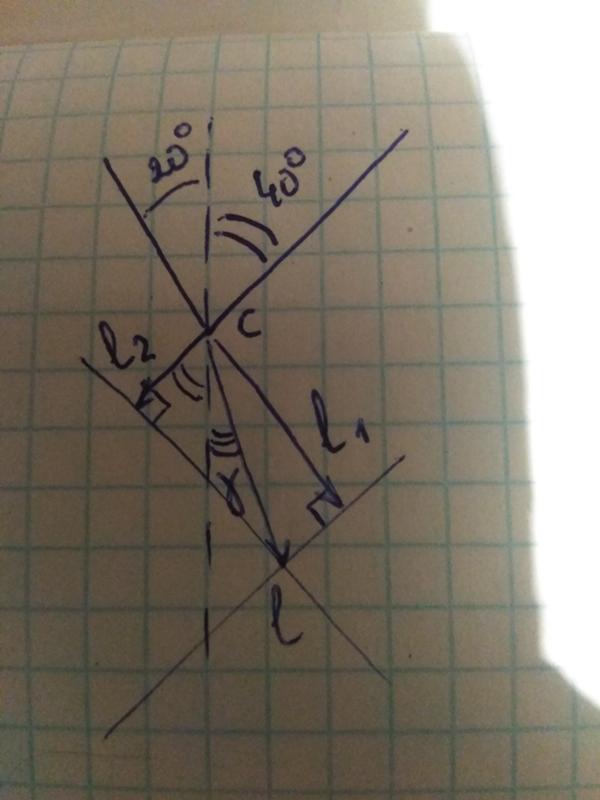
Как найти длину отрезка CL таким вот образом ( строим перпендикуляры от известных отрезков CL1, CL2, пересечение даёт отрезок СL(-общая гипотенуза двух прям-х треугольника), угол гамма неизвестен). Теорема косинусов, прошу, не предлагать. Заранее большое спасибо (угол L1CL2 равен 60*)


Короче. вот вам решение к чертежу предыдущего отвечавшего (Мало половин - это мой второй аккаунт). Будем считать, что я все правильно понял, а если нет - извините)))
1) Пусть для краткости AB=a, BC=b, AE=x, CE=y как на чертеже, угол АBC = 60
2) Тогда углы ADB и CFB равны 30
3) BD=2a, CD=2a-b
4) BF=2b, AF=2b-a
5) Треугольники AFE и ECD подобны — они прямоугольные и углы ADB и CFB равны 30 (см. пункт 2), кроме того другая пара углов там вертикальные
6) Из подобия этих треугольников имеем: x/y=AF/CD=(2b-a)/(2a-b)
7) Для общей гипотенузы имеем BE =L^2=a^2+x^2 = b^2+y^2
8) Вот собственно нам пара уравнений:
a^2+x^2 = b^2+y^2
x/y=(2b-a)/(2a-b)
9) Решаем их, всё находим. Можно через тангенсы, но вычислительно не проще:
y^2= 1/3*(2a-b)^2
Соответственно, L = √(y^2+ b^2)=√(4*(a^2+b^2-ab)*1/3)=2(√((1/3)*(a^2+b^2-ab))
При a=19, b=32 (или наоборот, без разницы)
L =2√259 Проверить не помешает
1) Пусть для краткости AB=a, BC=b, AE=x, CE=y как на чертеже, угол АBC = 60
2) Тогда углы ADB и CFB равны 30
3) BD=2a, CD=2a-b
4) BF=2b, AF=2b-a
5) Треугольники AFE и ECD подобны — они прямоугольные и углы ADB и CFB равны 30 (см. пункт 2), кроме того другая пара углов там вертикальные
6) Из подобия этих треугольников имеем: x/y=AF/CD=(2b-a)/(2a-b)
7) Для общей гипотенузы имеем BE =L^2=a^2+x^2 = b^2+y^2
8) Вот собственно нам пара уравнений:
a^2+x^2 = b^2+y^2
x/y=(2b-a)/(2a-b)
9) Решаем их, всё находим. Можно через тангенсы, но вычислительно не проще:
y^2= 1/3*(2a-b)^2
Соответственно, L = √(y^2+ b^2)=√(4*(a^2+b^2-ab)*1/3)=2(√((1/3)*(a^2+b^2-ab))
При a=19, b=32 (или наоборот, без разницы)
L =2√259 Проверить не помешает
Александр Ирканаев
Примечание в пункте 7)Для общей гипотенузы имеем BE =L^2=a^2+x^2 = b^2+y^2 пропущен символ степени у BE. Это мелочи, конечно, но всё равно
Чё-то не так... Если углы L1 и L2 90 градусов (по условию) то и угол С (см фото) должен быть 90 градусов, а не рисунке- (20+40) - 60 . Так не бывает.


Алексей Соловьёв
векторы не перпендикулярны
Нина Икаева
Л2 и Л1 не перпендикулярны, вот такую вот задачу подкинули, наверное, мне стоит, лучше начертить
Нина Икаева
Перпендикуляры проведены чтобы найти отрезок СL
Блин, ну у вас и чертежик. Вам же самому там ничего непонятно. Я вот не поленился, нарисовал. Теперь скажите мне применительно к моему чертежу - я правильно понял - дано AB, BC и угол АBC, а найти необходимо BE?
Я так то решил, просто хочу быть уверен, что условие правильно понял?
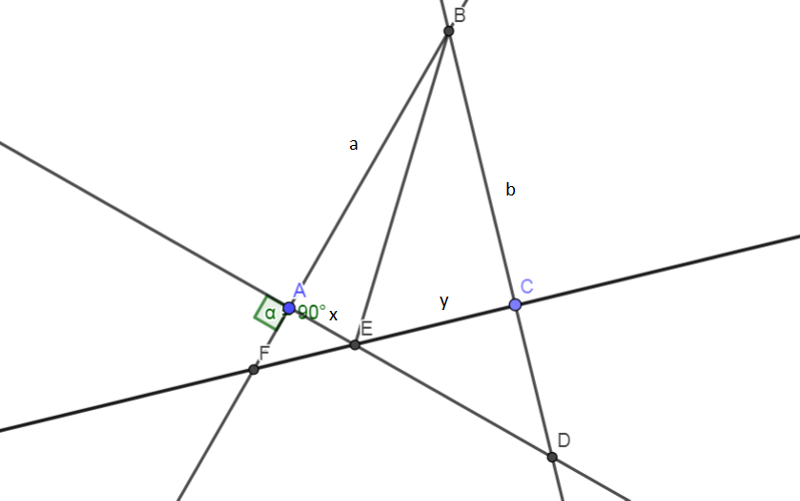
Я так то решил, просто хочу быть уверен, что условие правильно понял?

Нина Икаева
Вы правильно поняли условие задачи, прощееия за мою калиграфию). Это мой первый вопрос на маил. ру и в др. подобных форумах. Задачу скинул такой, какой и была мне задана, в следующий раз, постараюсь строить вопрос проще и понятнее
Похожие вопросы
- Один из углов прмоугольного треугольника равен 60градусам,а сумма гипотенузы и меньшего катета равна 72см.Найдите длину
- В основании прямой призмы лежит равнобедренный прямоугольный треугольник с гипотенузой 4√2см. Высота призмы равна 5см.
- Гипотенуза в равнобедренном прямоугольном треугольнике равна 31.2 см а высота проведенная к гипотенузе равна 15.6 см.
- Один из углов прямоугольного треугольника равен 30°, а сумма гипотенузы и меньшего катета-27 см.
- В треугольнике треугольнике abc сторона ac=6 ,bm- медиана bh- высота,bc=bm найдите длину отрезка ah
- Один из углов прямоугольного треугольника равен 30°, а сумма гипотенузы и меньшего катета – 27 см. далее.
- Вневписанная окружность и прямоугольный треугольник
- Синус острого угла В в прямоугольном треугольнике АВС равен 3√11/10 (это дробь) Найдите косинус угла В
- Найдите периметр прямоугольного треугольника,если один из его острых углов 60 градусов,а его катеты 4 и 4,6 см
- Уравнение катета и медианы прямоугольного треугольника.



